Machine and Deep Learning for Binary Classification

Python
Data Science
Author

Mohammad Savarmand

Published

2024 May 7

Overview

Abstract

In this project, I found a dataset (NYC Squirrel Dataset) with a binary column and decided to create a classification model using a Random Forest Tree, K-nearest neighbors, and the LSTM model. Before modeling, the dataset had to be tweaked a little. After tweaking the dataset and running the models, I solved several metrics that would determine the predictive power of the models. In short, the Random Forest Tree is the best model out of the three.

AUC:

RFT = 0.79, KNN = 0.61, LSTM = 0.74

External Packages

Overview of dataset

This project uses the 2018 NYC Central Park Squirrel Census dataset, which describes squirrels’ behaviors in different environments. The dataset was in rectangular format, which made the data preparation manageable. However, I had to ensure everything was represented numerically to accommodate some of the models being used (namely, the Deep Learning LSTM).

Machine Learning algorithms inside scikit-learn, such as Random Forest and KNN, are more forgiving about data types. With Pytorch, the model will only work if everything is numeric, which made me use different strategies for date/string columns.

Dataset Link

Code Analysis

Import Packages

Code 
import numpy as np
import pandas as pd
import polars as pl
import pytimetk as tk
import seaborn as sns

import random
import os
random.seed(1)

Examaining the data at high level

I am just trying to get a “feel” for this dataset. How large is it? Are there any NAs?

Code 
# https://data.cityofnewyork.us/Environment/2018-Central-Park-Squirrel-Census-Squirrel-Data/vfnx-vebw/about_data
df = pl.read_csv("files/2018_Central_Park_Squirrel_Census_-_Squirrel_Data_20240325.csv")
Code 
df.glimpse()
Rows: 3023
Columns: 31
$ X                                           <f64> -73.9561344937861, -73.9688574691102, -73.9742811484852, -73.9596413903948, -73.9702676472613, -73.9683613516225, -73.9541201789795, -73.9582694312289, -73.9674285955293, -73.9722500196844
$ Y                                           <f64> 40.7940823884086, 40.7837825208444, 40.775533619083, 40.7903128889029, 40.7762126854894, 40.7725908847499, 40.7931811701082, 40.7917367820255, 40.7829723919744, 40.7742879599026
$ Unique Squirrel ID                          <str> '37F-PM-1014-03', '21B-AM-1019-04', '11B-PM-1014-08', '32E-PM-1017-14', '13E-AM-1017-05', '11H-AM-1010-03', '36H-AM-1010-02', '33F-AM-1008-02', '21C-PM-1006-01', '11D-AM-1010-03'
$ Hectare                                     <str> '37F', '21B', '11B', '32E', '13E', '11H', '36H', '33F', '21C', '11D'
$ Shift                                       <str> 'PM', 'AM', 'PM', 'PM', 'AM', 'AM', 'AM', 'AM', 'PM', 'AM'
$ Date                                        <i64> 10142018, 10192018, 10142018, 10172018, 10172018, 10102018, 10102018, 10082018, 10062018, 10102018
$ Hectare Squirrel Number                     <i64> 3, 4, 8, 14, 5, 3, 2, 2, 1, 3
$ Age                                         <str> None, None, None, 'Adult', 'Adult', 'Adult', 'Adult', 'Adult', 'Adult', 'Adult'
$ Primary Fur Color                           <str> None, None, 'Gray', 'Gray', 'Gray', 'Cinnamon', 'Gray', 'Gray', 'Gray', 'Gray'
$ Highlight Fur Color                         <str> None, None, None, None, 'Cinnamon', 'White', None, None, None, 'Cinnamon'
$ Combination of Primary and Highlight Color  <str> '+', '+', 'Gray+', 'Gray+', 'Gray+Cinnamon', 'Cinnamon+White', 'Gray+', 'Gray+', 'Gray+', 'Gray+Cinnamon'
$ Color notes                                 <str> None, None, None, 'Nothing selected as Primary. Gray selected as Highlights. Made executive adjustments.', None, None, 'just outside hectare', None, None, None
$ Location                                    <str> None, None, 'Above Ground', None, 'Above Ground', None, 'Ground Plane', 'Ground Plane', 'Ground Plane', 'Above Ground'
$ Above Ground Sighter Measurement            <str> None, None, '10', None, None, None, 'FALSE', 'FALSE', 'FALSE', '30'
$ Specific Location                           <str> None, None, None, None, 'on tree stump', None, None, None, None, None
$ Running                                    <bool> False, False, False, False, False, False, False, False, False, False
$ Chasing                                    <bool> False, False, True, False, False, False, False, False, False, False
$ Climbing                                   <bool> False, False, False, False, False, False, False, False, False, True
$ Eating                                     <bool> False, False, False, True, False, False, False, False, False, False
$ Foraging                                   <bool> False, False, False, True, True, True, True, True, False, False
$ Other Activities                            <str> None, None, None, None, None, None, None, None, None, 'grooming'
$ Kuks                                       <bool> False, False, False, False, False, False, False, False, False, False
$ Quaas                                      <bool> False, False, False, False, False, False, False, False, False, False
$ Moans                                      <bool> False, False, False, False, False, False, False, False, False, False
$ Tail flags                                 <bool> False, False, False, False, False, False, False, False, True, False
$ Tail twitches                              <bool> False, False, False, False, False, True, False, False, True, False
$ Approaches                                 <bool> False, False, False, False, False, False, False, False, False, False
$ Indifferent                                <bool> False, False, False, False, False, True, False, True, False, True
$ Runs from                                  <bool> False, False, False, True, False, False, False, False, False, False
$ Other Interactions                          <str> None, None, None, None, None, None, None, None, None, None
$ Lat/Long                                    <str> 'POINT (-73.9561344937861 40.7940823884086)', 'POINT (-73.9688574691102 40.7837825208444)', 'POINT (-73.97428114848522 40.775533619083)', 'POINT (-73.9596413903948 40.7903128889029)', 'POINT (-73.9702676472613 40.7762126854894)', 'POINT (-73.9683613516225 40.7725908847499)', 'POINT (-73.9541201789795 40.7931811701082)', 'POINT (-73.9582694312289 40.7917367820255)', 'POINT (-73.9674285955293 40.7829723919744)', 'POINT (-73.9722500196844 40.7742879599026)'

Count the unique values in each column.

Code 
# Initialize an empty list to store the column names and another for the unique counts
column_names = []
unique_counts = []

# Loop through each column in df
for column_name in df.columns:
    # Calculate the number of unique values in the column
    unique_count = df.select(column_name).unique().height
    # Append the column name and unique count to their respective lists
    column_names.append(column_name)
    unique_counts.append(unique_count)

# Create a new DataFrame using a dictionary
df_unique_counts = pl.DataFrame({
    'Column Name': column_names,
    'Unique Values Count': unique_counts
})

df_unique_counts
shape: (31, 2)
Column Name Unique Values Count
str i64
"X" 3023
"Y" 3023
"Unique Squirrel ID" 3018
"Hectare" 339
"Shift" 2
… …
"Approaches" 2
"Indifferent" 2
"Runs from" 2
"Other Interactions" 198
"Lat/Long" 3023

Show the columns that only have 2 unique values (potential target columns to predict)

Code 
potential_targets = df_unique_counts.filter(pl.col('Unique Values Count')==2)
potential_targets
shape: (14, 2)
Column Name Unique Values Count
str i64
"Shift" 2
"Running" 2
"Chasing" 2
"Climbing" 2
"Eating" 2
… …
"Tail flags" 2
"Tail twitches" 2
"Approaches" 2
"Indifferent" 2
"Runs from" 2

Dealing With NA Values

Finding out how many NAs there are

Showing the percentage of NA values in each column.

Code 
import polars as pl

def calculate_na_percentages(df):
    column_names = []
    data_types = []
    na_percentages = []

    # Loop through each column in the DataFrame
    for column_name in df.columns:
        # Get the data type of the column
        data_type = str(df[column_name].dtype)
        # Calculate the total number of values in the column
        total_values = df[column_name].len()
        # Calculate the number of NA values in the column
        na_values = df[column_name].is_null().sum()
        # Calculate the percentage of NA values (NA count / total count * 100)
        na_percentage = (na_values / total_values) * 100
        # Append the results to their respective lists
        column_names.append(column_name)
        data_types.append(data_type)
        na_percentages.append(na_percentage)

    # Create a new DataFrame using a dictionary with the collected information
    df_na_percentages = pl.DataFrame({
        'Column Name': column_names,
        'Data Type': data_types,
        'Percent of NA In Column': na_percentages
    })

    return df_na_percentages


df1_na = calculate_na_percentages(df)
df1_na
shape: (31, 3)
Column Name Data Type Percent of NA In Column
str str f64
"X" "Float64" 0.0
"Y" "Float64" 0.0
"Unique Squirrel ID" "String" 0.0
"Hectare" "String" 0.0
"Shift" "String" 0.0
… … …
"Approaches" "Boolean" 0.0
"Indifferent" "Boolean" 0.0
"Runs from" "Boolean" 0.0
"Other Interactions" "String" 92.060867
"Lat/Long" "String" 0.0

Show the pecent of NA values in each column that has at least one NA value

Code 
df1_na.filter(pl.col('Percent of NA In Column')>0)
shape: (9, 3)
Column Name Data Type Percent of NA In Column
str str f64
"Age" "String" 4.002646
"Primary Fur Color" "String" 1.819385
"Highlight Fur Color" "String" 35.924578
"Color notes" "String" 93.979491
"Location" "String" 2.117102
"Above Ground Sighter Measureme… "String" 3.771088
"Specific Location" "String" 84.254052
"Other Activities" "String" 85.544161
"Other Interactions" "String" 92.060867

Removing NA Values

Removing columns where there are 30% or more NA values.

Code 
# Filtering out columns with more than 50% NAs
columns_to_drop = df1_na.filter(pl.col('Percent of NA In Column') > 30)['Column Name'].to_list()

# Create a new DataFrame by dropping these columns from the original DataFrame
df2 = df.drop(columns_to_drop)
Code 
df2_na = calculate_na_percentages(df2)
df2_na.filter(pl.col('Percent of NA In Column')>0)
shape: (4, 3)
Column Name Data Type Percent of NA In Column
str str f64
"Age" "String" 4.002646
"Primary Fur Color" "String" 1.819385
"Location" "String" 2.117102
"Above Ground Sighter Measureme… "String" 3.771088

Removing all rows with NA values.

Code 
df3 = df2.drop_nulls()
print(df2.shape)
print(df3.shape)
(3023, 26)
(2784, 26)

Final Check

Code 
df3_na = calculate_na_percentages(df3)
df3_na.filter(pl.col('Percent of NA In Column')>0)
shape: (0, 3)
Column Name Data Type Percent of NA In Column
str str f64

Fixing Date Column

There is a Date column that is considered numeric since the numbers are in the MMDDYYYY form, but I worry that the magnitude of the literal number will interfere with the interpretation of the date. For example, 10142018 -> 10152018 is just an increase of 1 day, but numerically, I added 10000 to the value. So, I split apart the date column into 4: Year, Month, Day, and Weekday.

Code 
df3_dtypes = df3.dtypes
df3_unique = set(df3_dtypes)
df3_unique
{Boolean, Float64, Int64, String}
Code 
import polars as pl

# Identify all string columns in df3
string_columns = [col for col, dtype in zip(df3.columns, df3.dtypes) if dtype == pl.Utf8]

string_columns
['Unique Squirrel ID',
 'Hectare',
 'Shift',
 'Age',
 'Primary Fur Color',
 'Combination of Primary and Highlight Color',
 'Location',
 'Above Ground Sighter Measurement',
 'Lat/Long']
Code 
df3_string_only = df3.select(string_columns)

Extracting year, month, day, weekday from original “Date” column into 4 new columns

Code 
import polars as pl

# Convert integer dates to strings, then parse as dates assuming format is MMDDYYYY
df3_2 = df3.with_columns(
    pl.col("Date").cast(pl.Utf8).str.strptime(pl.Date, "%m%d%Y")
)

# Extracting components for further analysis or features
df3_3 = df3_2.with_columns([
    pl.col("Date").dt.year().alias("Year"),
    pl.col("Date").dt.month().alias("Month"),
    pl.col("Date").dt.day().alias("Day"),
    pl.col("Date").dt.weekday().alias("Weekday")  # Monday is 0 and Sunday is 6
])

# Step 2: Remove the original 'Lat/Long' column
df3_4 = df3_3.drop("Lat/Long")

# Define the priority columns that should appear first
priority_columns = ['X', 'Y', 'Date', 'Year', 'Month', 'Day', 'Weekday']

# Get a list of all other columns that are not in the priority list
other_columns = [col for col in df3_4.columns if col not in priority_columns]

# Combine the lists to create the new column order
new_column_order = priority_columns + other_columns

# Select columns in the new order
df3_5 = df3_4.select(new_column_order)
df4 = df3_5.drop('Date') 


# Display the DataFrame to check the results
df4.head()
shape: (5, 28)
X Y Year Month Day Weekday Unique Squirrel ID Hectare Shift Hectare Squirrel Number Age Primary Fur Color Combination of Primary and Highlight Color Location Above Ground Sighter Measurement Running Chasing Climbing Eating Foraging Kuks Quaas Moans Tail flags Tail twitches Approaches Indifferent Runs from
f64 f64 i32 i8 i8 i8 str str str i64 str str str str str bool bool bool bool bool bool bool bool bool bool bool bool bool
-73.95412 40.793181 2018 10 10 3 "36H-AM-1010-02" "36H" "AM" 2 "Adult" "Gray" "Gray+" "Ground Plane" "FALSE" false false false false true false false false false false false false false
-73.958269 40.791737 2018 10 8 1 "33F-AM-1008-02" "33F" "AM" 2 "Adult" "Gray" "Gray+" "Ground Plane" "FALSE" false false false false true false false false false false false true false
-73.967429 40.782972 2018 10 6 6 "21C-PM-1006-01" "21C" "PM" 1 "Adult" "Gray" "Gray+" "Ground Plane" "FALSE" false false false false false false false false true true false false false
-73.97225 40.774288 2018 10 10 3 "11D-AM-1010-03" "11D" "AM" 3 "Adult" "Gray" "Gray+Cinnamon" "Above Ground" "30" false false true false false false false false false false false true false
-73.969506 40.782351 2018 10 13 6 "20B-PM-1013-05" "20B" "PM" 5 "Adult" "Gray" "Gray+White" "Ground Plane" "FALSE" false false false false true false false false false false false true false
Code 
print(df3.shape)
print(df4.shape)
(2784, 26)
(2784, 28)

One Hot Encoding

I needed to convert string columns such as “Primary Fur Color” into numerical columns. Since my dataset is small, I employed one hot encoding. If the dataset had thousands of string columns and millions of rows, I would use Label Encoding even though One Hot Encoding is preferred since there is no hierarchy of numbers.

Code 
df4_pandas = df4.to_pandas()

# Identify all string columns in the pandas DataFrame
string_columns = [col for col in df4_pandas.columns if df4_pandas[col].dtype == 'object']
Code 
# Move string columns to the end of the DataFrame
non_string_columns = [col for col in df4_pandas.columns if col not in string_columns]
new_column_order = non_string_columns + string_columns  # Concatenate lists to reorganize
df4_pandas = df4_pandas[new_column_order]
Code 
# Perform one-hot encoding on the string columns and save the result to df5
df5_pandas = pd.get_dummies(df4_pandas, columns=string_columns)
df5_pandas.shape
(2784, 3204)

Investigating why there are 3000+ columns

Code 
string_unique_counts = pd.DataFrame({
    'Column Name': string_columns,
    'Unique Values Count': [df4_pandas[col].nunique() for col in string_columns]
})

# Display the DataFrame
print(string_unique_counts)
                                  Column Name  Unique Values Count
0                          Unique Squirrel ID                 2779
1                                     Hectare                  334
2                                       Shift                    2
3                                         Age                    3
4                           Primary Fur Color                    3
5  Combination of Primary and Highlight Color                   21
6                                    Location                    2
7            Above Ground Sighter Measurement                   40

Redo One Hot Encoding

The initial One Hot Encoding had a ridiculous number of columns, but I fixed that by removing the Squirrel ID column, which would not have been useful for modeling anyway.

425 Columns is much more reasonable than 3000+ columns

Code 
# Redo the previous steps but drop the Unique Squirrel ID since it will not help with the modeling
df4 = df4.drop("Unique Squirrel ID")

df4_pandas = df4.to_pandas()

# Identify all string columns in the pandas DataFrame
string_columns = [col for col in df4_pandas.columns if df4_pandas[col].dtype == 'object']

# Move string columns to the end of the DataFrame
non_string_columns = [col for col in df4_pandas.columns if col not in string_columns]
new_column_order = non_string_columns + string_columns  # Concatenate lists to reorganize
df4_pandas = df4_pandas[new_column_order]

# Perform one-hot encoding on the string columns and save the result to df5
df5_pandas = pd.get_dummies(df4_pandas, columns=string_columns)
df5_pandas.shape
(2784, 425)
Code 
df5 = pl.from_pandas(df5_pandas)

Choose Target Column (Eating)

Code 
# Define the priority columns that should appear first
priority_columns = ['Eating']

# Get a list of all other columns that are not in the priority list
other_columns = [col for col in df5.columns if col not in priority_columns]

# Combine the lists to create the new column order
new_column_order = priority_columns + other_columns

df6 = df5.select(new_column_order)
df6
shape: (2_784, 425)
Eating X Y Year Month Day Weekday Hectare Squirrel Number Running Chasing Climbing Foraging Kuks Quaas Moans Tail flags Tail twitches Approaches Indifferent Runs from Hectare_01A Hectare_01B Hectare_01C Hectare_01D Hectare_01E Hectare_01F Hectare_01G Hectare_01H Hectare_01I Hectare_02A Hectare_02B Hectare_02C Hectare_02D Hectare_02E Hectare_02F Hectare_02G Hectare_02H … Above Ground Sighter Measurement_100 Above Ground Sighter Measurement_11 Above Ground Sighter Measurement_12 Above Ground Sighter Measurement_13 Above Ground Sighter Measurement_14 Above Ground Sighter Measurement_15 Above Ground Sighter Measurement_16 Above Ground Sighter Measurement_17 Above Ground Sighter Measurement_18 Above Ground Sighter Measurement_180 Above Ground Sighter Measurement_19 Above Ground Sighter Measurement_2 Above Ground Sighter Measurement_20 Above Ground Sighter Measurement_23 Above Ground Sighter Measurement_24 Above Ground Sighter Measurement_25 Above Ground Sighter Measurement_28 Above Ground Sighter Measurement_3 Above Ground Sighter Measurement_30 Above Ground Sighter Measurement_31 Above Ground Sighter Measurement_33 Above Ground Sighter Measurement_35 Above Ground Sighter Measurement_4 Above Ground Sighter Measurement_40 Above Ground Sighter Measurement_45 Above Ground Sighter Measurement_5 Above Ground Sighter Measurement_50 Above Ground Sighter Measurement_55 Above Ground Sighter Measurement_6 Above Ground Sighter Measurement_60 Above Ground Sighter Measurement_65 Above Ground Sighter Measurement_7 Above Ground Sighter Measurement_70 Above Ground Sighter Measurement_8 Above Ground Sighter Measurement_80 Above Ground Sighter Measurement_9 Above Ground Sighter Measurement_FALSE
bool f64 f64 i32 i8 i8 i8 i64 bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool … bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool bool
false -73.95412 40.793181 2018 10 10 3 2 false false false true false false false false false false false false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
false -73.958269 40.791737 2018 10 8 1 2 false false false true false false false false false false true false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
false -73.967429 40.782972 2018 10 6 6 1 false false false false false false false true true false false false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
false -73.97225 40.774288 2018 10 10 3 3 false false true false false false false false false false true false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false true false false false false false false false false false false false false false false false false false false
false -73.969506 40.782351 2018 10 13 6 5 false false false true false false false false false false true false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
… … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … …
false -73.964544 40.78116 2018 10 18 4 2 false false false true false false false false false false false true false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
true -73.963943 40.790868 2018 10 7 7 4 false false false true false false false false false false false true false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
false -73.970402 40.78256 2018 10 13 6 5 false false false true false false false false false false true false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
true -73.966587 40.783678 2018 10 12 5 7 false false false true false false false false false false true false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
true -73.975479 40.76964 2018 10 12 5 1 false false false true false false false false false true false false false false false false false false false false false false false false false false false false false … false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false false true
Code 
df6_dtypes = df6.dtypes
df6_unique = set(df6_dtypes)
df6_unique
{Boolean, Float64, Int32, Int64, Int8}

Modeling

Cross Validation for Machine Learning Algorithms

Since sci-kit learn is extremely friendly and allows for easy switching between models, I made a function that takes four inputs: X, y, model, and n_splits. X and y are the features and targets, respectively. ‘model’ is the sci-kit learn classification class, which is easily interchangeable thanks to its design. ‘n_splits’ is an integer representing the number of folds for cross-validation.

I had to calculate the TP, TN, FP, FN, and roc_auc inside that same function since it would have been challenging to do it outside the function.

I created a second function to satisfy the project’s requirements that calculate the other metrics.

Then, I made some ROC graphs of the last fold (an ROC for all folds would be cluttered) and saved them to the graphs subdirectory.

Code 
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import KFold

def perform_cross_validation(X, y, model, n_splits=10):
    kf = KFold(n_splits=n_splits, shuffle=True, random_state=1)
    results_df = pd.DataFrame()
    roc_auc_list = []

    # Variables to hold the last fold's ROC data for plotting
    last_fpr, last_tpr, last_roc_auc = None, None, None

    for i, (train_index, test_index) in enumerate(kf.split(X)):
        X_train, X_test = X.iloc[train_index], X.iloc[test_index]
        y_train, y_test = y.iloc[train_index], y.iloc[test_index]

        model.fit(X_train, y_train)
        y_scores = model.predict_proba(X_test)[:, 1]  # Assuming binary classification

        # Calculate ROC AUC
        fpr, tpr, _ = roc_curve(y_test, y_scores)
        roc_auc = auc(fpr, tpr)
        roc_auc_list.append(roc_auc)

        if i == n_splits - 1:  # Save last fold's ROC data
            last_fpr, last_tpr, last_roc_auc = fpr, tpr, roc_auc

        # Calculate confusion matrix components manually
        y_pred = model.predict(X_test)
        TP = np.sum((y_pred == 1) & (y_test == 1))
        TN = np.sum((y_pred == 0) & (y_test == 0))
        FP = np.sum((y_pred == 1) & (y_test == 0))
        FN = np.sum((y_pred == 0) & (y_test == 1))

        fold_results = pd.DataFrame({
            'Model Name': model.__class__.__name__,
            'Fold Number': i + 1,
            'TP': [TP],
            'TN': [TN],
            'FP': [FP],
            'FN': [FN],
            'ROC AUC': [roc_auc]
        })
        results_df = pd.concat([results_df, fold_results], ignore_index=True)

    # Append a row for the average values
    average_auc = np.mean(roc_auc_list)
    results_df = pd.concat([results_df, pd.DataFrame({'Model Name': model.__class__.__name__, 'Fold Number': 'Average', 'ROC AUC': [average_auc]})], ignore_index=True)
    return results_df, last_fpr, last_tpr, last_roc_auc
Code 
import pandas as pd

def calculate_all_metrics(results_df):
    # Calculate accuracy
    results_df['Accuracy'] = (results_df['TP'] + results_df['TN']) / (results_df['TP'] + results_df['TN'] + results_df['FP'] + results_df['FN'])
    
    # Calculate precision
    results_df['Precision'] = results_df['TP'] / (results_df['TP'] + results_df['FP'])
    
    # Calculate recall. This is the same as TPR
    results_df['Recall'] = results_df['TP'] / (results_df['TP'] + results_df['FN'])
    
    # Calculate F1 score
    results_df['F1 Score'] = 2 * (results_df['Precision'] * results_df['Recall']) / (results_df['Precision'] + results_df['Recall'])
    
    # Calculate specificity. This is the same as TNR
    results_df['Specificity'] = results_df['TN'] / (results_df['TN'] + results_df['FP'])
    
    # Calculate false positive rate (FPR)
    results_df['FPR'] = results_df['FP'] / (results_df['TN'] + results_df['FP'])

    # Calculate false negative rate (FNR)
    results_df['FNR'] = results_df['FN'] / (results_df['FN'] + results_df['TP'])

    # Calculate negative predictive value (NPV)
    results_df['NPV'] = results_df['TN'] / (results_df['TN'] + results_df['FN'])

    # Calculate error rate
    results_df['Error Rate'] = (results_df['FP'] + results_df['FN']) / (results_df['TP'] + results_df['FP'] + results_df['FN'] + results_df['TN'])

    
    return results_df
Code 
# Convert Polars DataFrame to Pandas DataFrame (if df6 is a Polars DataFrame)
df6_pandas = df6.to_pandas()

# Separate target variable 'y' and features 'X'
y = df6_pandas.iloc[:, 0]  # First column as target
X = df6_pandas.iloc[:, 1:]  # Remaining columns as features

Random Forest

Code 
from sklearn.ensemble import RandomForestClassifier
model_rf = RandomForestClassifier(n_estimators=100, random_state=1)
cross_df_rf = perform_cross_validation(X, y, model_rf)
metrics_df_rf = calculate_all_metrics(cross_df_rf[0])

average_row = metrics_df_rf.iloc[:-1, 2:].mean()

metrics_df_rf.iloc[-1, 2:] = average_row  
metrics_df_rf_2 = np.round(metrics_df_rf, 4)
Code 
metrics_df_rf_2.head()
Model Name Fold Number TP TN FP FN ROC AUC Accuracy Precision Recall F1 Score Specificity FPR FNR NPV Error Rate
0 RandomForestClassifier 1 22.0 201.0 7.0 49.0 0.7720 0.7993 0.7586 0.3099 0.4400 0.9663 0.0337 0.6901 0.8040 0.2007
1 RandomForestClassifier 2 23.0 198.0 5.0 53.0 0.7816 0.7921 0.8214 0.3026 0.4423 0.9754 0.0246 0.6974 0.7888 0.2079
2 RandomForestClassifier 3 22.0 203.0 2.0 52.0 0.8267 0.8065 0.9167 0.2973 0.4490 0.9902 0.0098 0.7027 0.7961 0.1935
3 RandomForestClassifier 4 19.0 199.0 5.0 56.0 0.8106 0.7814 0.7917 0.2533 0.3838 0.9755 0.0245 0.7467 0.7804 0.2186
4 RandomForestClassifier 5 19.0 214.0 6.0 39.0 0.8432 0.8381 0.7600 0.3276 0.4578 0.9727 0.0273 0.6724 0.8458 0.1619
Code 
# import matplotlib.pyplot as plt
# 
# plt.figure()
# plt.plot(cross_df_rf[1], cross_df_rf[2], color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % cross_df_rf[3])
# plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
# plt.xlim([0.0, 1.0])
# plt.ylim([0.0, 1.05])
# plt.xlabel('False Positive Rate')
# plt.ylabel('True Positive Rate')
# plt.title('Random Forest ROC (Last Fold)')
# plt.legend(loc="lower right")


# plt.savefig('graphs/squirrel_ml_dl/RF-roc_curve_last_fold.png')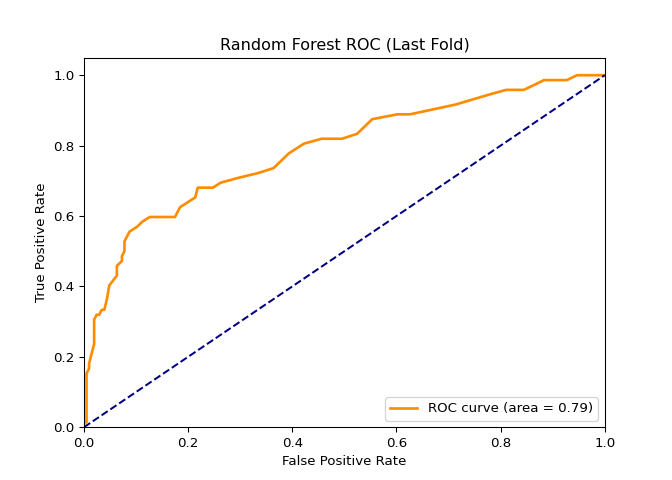

KNN

Code 
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler

# Convert Polars DataFrame to Pandas DataFrame (if df6 is a Polars DataFrame)
df6_pandas = df6.to_pandas()

# Separate target variable 'y' and features 'X'
y = df6_pandas.iloc[:, 0]  # First column as the target
X = df6_pandas.iloc[:, 1:]  # Remaining columns as features

# Initialize the scaler
scaler = StandardScaler()

# Fit and transform the feature data
X_scaled = scaler.fit_transform(X)

knn_model = KNeighborsClassifier(n_neighbors=5)
cross_df_knn = perform_cross_validation(X, y, knn_model)

metrics_df_knn = np.round(calculate_all_metrics(cross_df_knn[0]), 4)
average_row_knn = metrics_df_rf.iloc[:-1, 2:].mean()
metrics_df_knn.iloc[-1, 2:] = average_row_knn 

metrics_df_knn_2 = np.round(metrics_df_knn, 4)
Code 
metrics_df_knn.tail()
Model Name Fold Number TP TN FP FN ROC AUC Accuracy Precision Recall F1 Score Specificity FPR FNR NPV Error Rate
6 KNeighborsClassifier 7 16.0 183.0 24.0 55.0 0.636500 0.715800 0.400000 0.225400 0.288300 0.884100 0.115900 0.774600 0.768900 0.284200
7 KNeighborsClassifier 8 14.0 184.0 15.0 65.0 0.669800 0.712200 0.482800 0.177200 0.259300 0.924600 0.075400 0.822800 0.739000 0.287800
8 KNeighborsClassifier 9 16.0 198.0 13.0 51.0 0.662500 0.769800 0.551700 0.238800 0.333300 0.938400 0.061600 0.761200 0.795200 0.230200
9 KNeighborsClassifier 10 18.0 194.0 12.0 54.0 0.614000 0.762600 0.600000 0.250000 0.352900 0.941700 0.058300 0.750000 0.782300 0.237400
10 KNeighborsClassifier Average 20.9 200.6 6.8 50.1 0.794545 0.795619 0.767262 0.295261 0.424244 0.967228 0.032772 0.704739 0.800113 0.204381
Code 
# import matplotlib.pyplot as plt
# 
# plt.figure()
# plt.plot(cross_df_knn[1], cross_df_knn[2], color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % cross_df_knn[3])
# plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
# plt.xlim([0.0, 1.0])
# plt.ylim([0.0, 1.05])
# plt.xlabel('False Positive Rate')
# plt.ylabel('True Positive Rate')
# plt.title('KNN ROC (Last Fold)')
# plt.legend(loc="lower right")


# plt.savefig('graphs/squirrel_ml_dl/KNN-roc_curve_last_fold.png')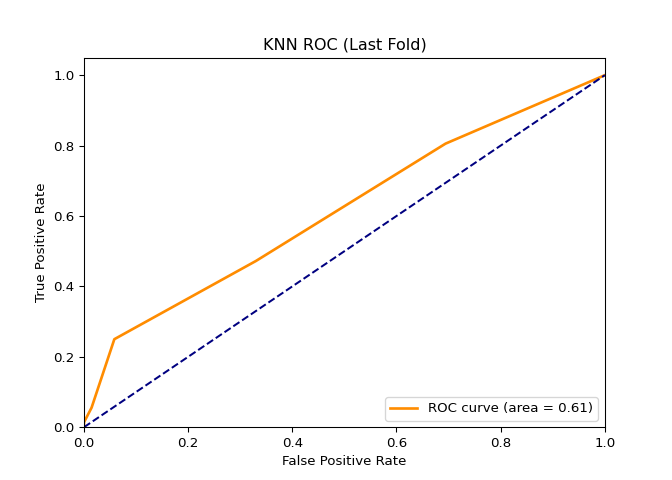

### LSTM

Choosing Packages

I chose to use Pytorch since it is one of the popular neural network packages. I have also had the most experience with Pytorch, and I knew that this package could satisfy the deep learning portion of the project.

Code 
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset, SubsetRandomSampler
from sklearn.model_selection import KFold
from sklearn.metrics import roc_curve, auc

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

Define LSTM Model

To create an NN in Pytorch, I needed to define a class. I also need a constructor to initialize the LSTMClassifier when defining a class. After specifying the constructor, I need to call it to handle the underlying initialization. Then, I calculated the number of features and hidden layers. Next, I created an LSTM module followed by a linear module. I only wanted to use LSTM but needed to transform the output to a specific size to get the correct output. So, the model has two layers, and I can adjust the neuron count when modeling. (The sigmoid activation function is not present because of the optimizer I used)

With every neural network there needs to be a forward pass defined. h0 is a hidden state, c0 is the cell state, and both start at 0. When forward and back propagation occurs, the zeroes will change into the weights designated by the optimizer.

Code 
class LSTMClassifier(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, num_classes):
        super(LSTMClassifier, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
        self.fc = nn.Linear(hidden_size, num_classes)

    def forward(self, x):
        h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
        c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
        out, _ = self.lstm(x, (h0, c0))
        out = self.fc(out[:, -1, :])
        return out

Make a metrics function

I could not use the old metrics function since Pytorch’s data types are vastly different from sci-kit learn, but these encompass all of module 8’s metrics.

Code 
# Function to calculate metrics manually
def calculate_metrics(y_true, y_pred, fold):
    TP = TN = FP = FN = 0
    for true, pred in zip(y_true, y_pred):
        if true == pred == 1:
            TP += 1
        elif true == pred == 0:
            TN += 1
        elif true == 0 and pred == 1:
            FP += 1
        elif true == 1 and pred == 0:
            FN += 1

    accuracy = (TP + TN) / (TP + TN + FP + FN) if (TP + TN + FP + FN) != 0 else 0
    precision = TP / (TP + FP) if (TP + FP) != 0 else 0
    recall = TP / (TP + FN) if (TP + FN) != 0 else 0
    f1_score = 2 * (precision * recall) / (precision + recall) if (precision + recall) != 0 else 0
    specificity = TN / (TN + FP) if (TN + FP) != 0 else 0
    fpr = FP / (FP + TN) if (FP + TN) != 0 else 0
    fnr = FN / (FN + TP) if (FN + TP) != 0 else 0 
    npv = TN / (TN + FN) if (TN + FN) != 0 else 0
    fdr = FP / (FP + TP) if (FP + TP) != 0 else 0
    error_rate = (FP + FN) / (TP + FP + FN + TN) if (TP + FP + FN + TN) != 0 else 0 
    return pd.DataFrame({
        'Fold': [fold],
        'TP': [TP], 'TN': [TN], 'FP': [FP], 'FN': [FN],
        'Accuracy': [accuracy], 'Precision': [precision], 'Recall': [recall],
        'F1 Score': [f1_score], 'Specificity': [specificity],
        'FPR': [fpr], 'FNR': [fnr], 'NPV': [npv], 'FDR': [fdr],'Error Rate': [error_rate]
    })

Prepare the data

Similar to KNN, I scaled the data since neural networks are simply a large volume of mathematical computations, so it’s a good idea to ensure that the data doesn’t have huge differences in magnitude.

Code 
# Setup for the LSTM model
data_np = scaler.fit_transform(X) # Assuming X is your feature matrix
data = torch.tensor(data_np, dtype=torch.float32).unsqueeze(1)  # Add sequence dimension
labels = torch.tensor(y, dtype=torch.long)  # Assuming y is your target vector
dataset = TensorDataset(data, labels)

Training and Validation Loop

I use KFold from Scikit Learn to get the partitions for my pandas dataframe. Since Pytorch has some issues working with pandas and Scikit Learn, I use DataLoader to create samples using the indices generated by KFold. Then, DataLoader handles the cross-validation for Pytorch.

I briefly mentioned that I did not add the Sigmoid activation function at the end of the neural network even though I am doing a binary classification. This is because the criterion “CrossEntropyLoss” implicitly does that for me. The optimizer is an altered version of gradient descent, but the general idea is that the for loop tries to minimize cross-entropy. This is what we define as making the model better.

During each of the epochs, the model is trained on batches of data, where it computes the loss, performs backpropagation, and updates the model weights. After training, the model is evaluated in a non-training mode to calculate validation loss, accuracy, and ROC-AUC metrics, capturing predictions and their probabilities to assess performance across various thresholds.

Code 
kfold = KFold(n_splits=10, shuffle=True, random_state=42)
# Graphs were generated using 200 epochs but for the sake of rendering speed, the epoch is set to 1 here.
epoch_num = 1
results_list = []
metrics_list = []
roc_data = []

for fold, (train_idx, val_idx) in enumerate(kfold.split(dataset)):
    train_subsampler = SubsetRandomSampler(train_idx)
    val_subsampler = SubsetRandomSampler(val_idx)
    train_loader = DataLoader(dataset, batch_size=32, sampler=train_subsampler)
    val_loader = DataLoader(dataset, batch_size=32, sampler=val_subsampler)

    model = LSTMClassifier(424, 128, 2, 2).to(device)  # Adjust class count as needed
    criterion = nn.CrossEntropyLoss()
    optimizer = optim.Adam(model.parameters(), lr=0.01)

    for epoch in range(epoch_num):  # Adjust number of epochs as needed
        model.train()
        total_loss = 0
        for inputs, targets in train_loader:
            inputs, targets = inputs.to(device), targets.to(device)
            optimizer.zero_grad()
            outputs = model(inputs)
            loss = criterion(outputs, targets)
            loss.backward()
            optimizer.step()
            total_loss += loss.item()

        # Validation
        model.eval()
        val_loss = 0
        y_true = []
        y_pred = []
        y_scores = []  # Store probabilities for ROC calculation
        with torch.no_grad():
            for inputs, targets in val_loader:
                inputs, targets = inputs.to(device), targets.to(device)
                outputs = model(inputs)
                _, predicted = torch.max(outputs.data, 1)
                y_pred.extend(predicted.cpu().numpy())
                y_true.extend(targets.cpu().numpy())
                y_scores.extend(outputs.softmax(dim=1).cpu().numpy()[:, 1])
                val_loss += criterion(outputs, targets).item()

        fpr, tpr, _ = roc_curve(y_true, y_scores)
        roc_auc = auc(fpr, tpr)
        roc_data.append({'Fold': fold + 1, 'Epoch': epoch + 1, 'FPR': fpr, 'TPR': tpr, 'ROC AUC': roc_auc})
        
        val_acc = 100 * (predicted == targets).sum().item() / targets.size(0)
        results_list.append({
            'Fold': fold + 1,
            'Epoch': epoch + 1,
            'Loss': total_loss / len(train_loader),
            'Val Loss': val_loss / len(val_loader),
            'Val Acc': val_acc,
            'ROC AUC': roc_auc
        })

    metrics_df = calculate_metrics(y_true, y_pred, fold+1)
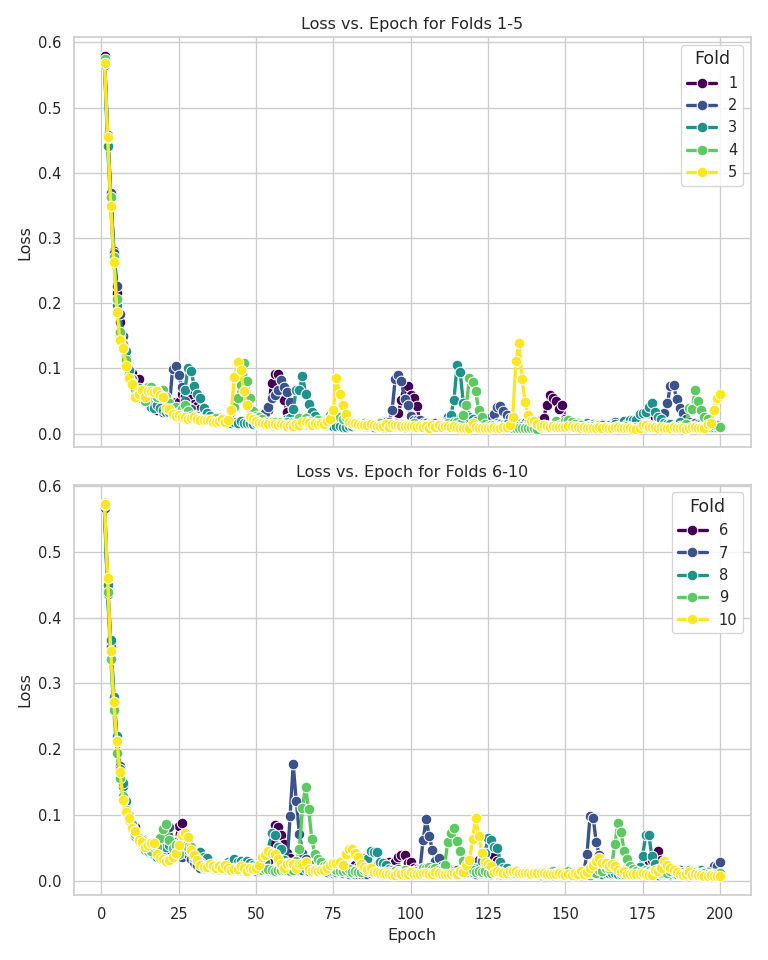
    metrics_list.append(metrics_df)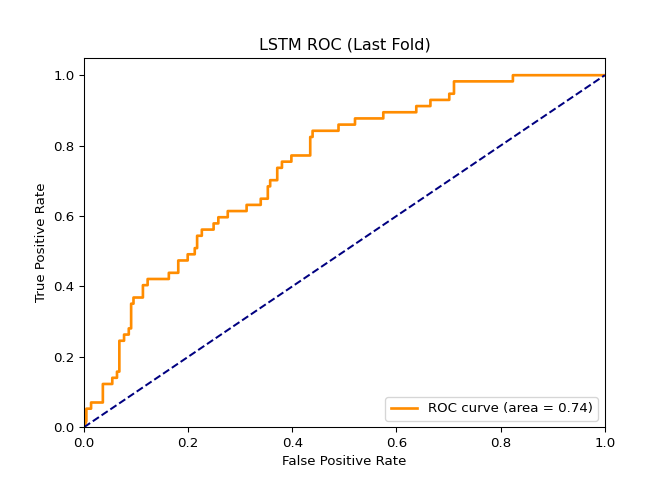

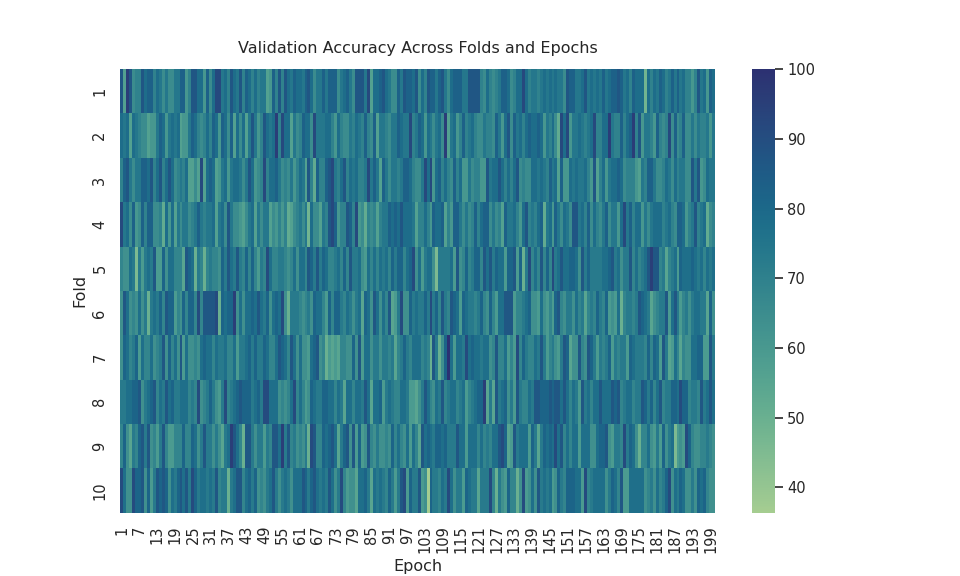
Storing Results

Code 
# Prepare dataframes for output
epoch_results_df = pd.DataFrame(results_list)
metrics_df = pd.concat(metrics_list, ignore_index=True)
roc_df = pd.DataFrame(roc_data)

Plots

ROC/AUC

Conclusion

The Random Forest Classifier was the best model, which was expected because it can deal with complicated and small datasets using the ensemble method, which consists of bootstrapping + aggregation (bagging).

KNN is a simpler model than RFT because it only uses distances between points to make predictions, whereas RFT uses bagging, a more complicated algorithm that is more suitable for a complex dataset.

Even though LSTM scored an AUC of .74, it is worse than KNN. Graphing the Loss vs. Epoch and Fold vs. Epoch vs. Accuracy graphs shows that LSTM is unstable. I expected the Loss vs Epoch graph to have a nice reverse exponential curve, but there were so many peaks in the graph. Also, I expected the heatmap to have a smooth gradient transitioning from light blue to dark blue. The heatmap looked like the colors were randomized, meaning it never stabilized after 200 epochs.

This could mean two things. This could mean that I needed to use more epochs or that this dataset is unsuitable for deep learning models. It could be either, but I am leaning more towards the latter. The mechanism behind deep learning is optimization. Gradient descent is the primary driver of deep learning, and in this case, it is “optimizing” or finding the minimum of the cross-entropy criterion. A weakness of gradient descent is that models can get stuck in local minimums or saddle points, halting model improvement. This weakness is usually mitigated by proper datasets with many more columns and rows, reducing the probability of hitting those local minimums or saddle points. This dataset is small, meaning the likelihood of hitting a local minimum is significant, so LSTM performed the worst of the three.

Thumbnail icon from Freepik